Какие методы оптимизации применяют при решении задач линейного целочисленного программирования

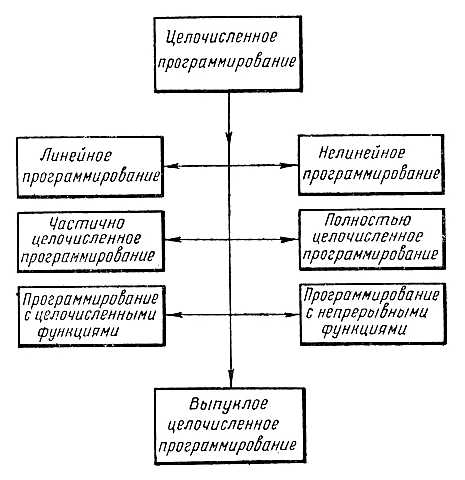
Задачи линейного целочисленного программирования встречаются во многих областях, таких как производство, логистика, финансы и многие другие. Они связаны с поиском оптимального решения в задачах, где решениями могут быть только целые числа. Решение таких задач является сложной задачей оптимизации, требующей применения специальных методов и алгоритмов.

Существует несколько основных методов оптимизации, которые можно использовать для решения задач линейного целочисленного программирования. Один из таких методов — метод ветвей и границ. Он основан на рекурсивном разбиении исходной задачи на более простые подзадачи. При этом в каждой подзадаче осуществляется перебор всех возможных решений, и выбирается наилучшее из них. Метод ветвей и границ позволяет найти точное решение задачи, но при больших размерах задачи может быть вычислительно сложным.

Другой метод оптимизации — метод симплекс-метода. Он основан на применении алгоритма симплекс-метода для решения релаксированной задачи линейного программирования. Затем полученное решение аппроксимируется целыми числами с использованием различных техник. Метод симплекс-метода является эффективным и позволяет решать задачи большого размера, но его точность может быть ниже, чем у метода ветвей и границ.

Важно подобрать наиболее подходящий метод оптимизации в зависимости от размера задачи, требуемой точности решения и доступных вычислительных ресурсов. Кроме того, решение задач линейного целочисленного программирования может быть улучшено путем применения различных техник, таких как редукция и динамическое программирование.

Что такое линейное целочисленное программирование и его особенности

Основной особенностью ЛЦП является наличие ограничений на значения переменных, которые могут быть только целыми числами. Это делает решение таких задач более сложным, так как требуется найти оптимальное целочисленное решение.

Применение ЛЦП находит во многих сферах, включая экономику, производственное планирование, логистику, транспортные проблемы, расписание занятий и другие.

Математическая формулировка ЛЦП

ЛЦП может быть сформулирована следующим образом:

Минимизировать: c1x1 + c2x2 + … + cnxn

При ограничениях:

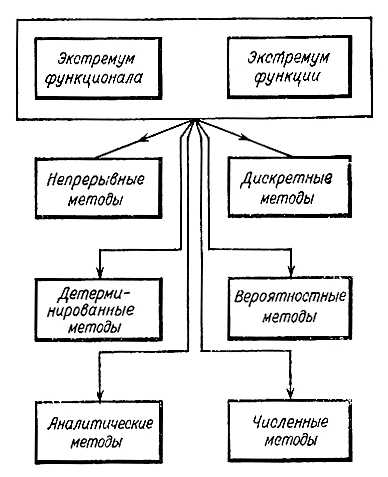
a11x1 + a12x2 + … + a1nxn ≤ b1

a21x1 + a22x2 + … + a2nxn ≤ b2

…

amx1 + am2x2 + … + amnxn ≤ bm

x1, x2, …, xn ∈ Z

Решение ЛЦП

Решение задач ЛЦП может быть достигнуто различными методами, включая полный перебор, методы ветвей и границ, методы динамического программирования, эвристические алгоритмы и другие.

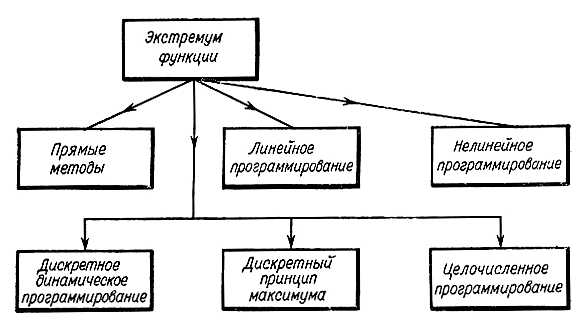
Однако, из-за NP-полноты задач ЛЦП, поиск точного оптимального решения может быть вычислительно сложным и требовать больших вычислительных ресурсов. В связи с этим часто используются эвристические алгоритмы, которые дают приближенное решение за приемлемое время.

Описание методов оптимизации для решения задач линейного целочисленного программирования

Существует несколько основных методов оптимизации для решения задач линейного целочисленного программирования:

1. Метод полного перебора (brute-force)

Этот метод заключается в переборе всех возможных комбинаций значений целочисленных переменных и выборе оптимального решения. Он гарантированно дает точное решение, но требует большого количества вычислительных ресурсов, особенно при большом числе переменных.

2. Метод ветвей и границ (branch and bound)

Этот метод основан на разбиении задачи на более простые подзадачи и последовательном их решении. При этом используется оценка нижней границы для каждой подзадачи, которая позволяет отсекать неперспективные ветви поиска. Метод ветвей и границ обычно даёт приближенное решение, но работает гораздо быстрее метода полного перебора.

3. Метод динамического программирования (dynamic programming)

Этот метод основан на разбиении задачи на более простые подзадачи и использовании найденных решений для нахождения оптимального решения исходной задачи. Метод динамического программирования может использоваться для решения определенных классов задач линейного целочисленного программирования, основываясь на определенных свойствах и структуре задачи.

4. Метод ветвей и цены (branch and price)

Этот метод является комбинацией метода ветвей и границ с методом динамического программирования. Он используется при решении задач, где количество переменных слишком большое для применения метода ветвей и границ. Метод ветвей и цены позволяет эффективно находить оптимальное решение, основываясь на нескольких наборах переменных.

Каждый из перечисленных методов имеет свои достоинства и ограничения, и выбор метода оптимизации зависит от конкретной задачи и требований к решению. Разработка и улучшение методов оптимизации для решения задач линейного целочисленного программирования является активной областью исследований.

Вопрос-ответ:

Что такое задача линейного целочисленного программирования?

Задача линейного целочисленного программирования — это математическая задача оптимизации, которая заключается в поиске максимального или минимального значения линейной целочисленной функции от нескольких переменных при условии, что значения этих переменных являются целыми числами.

Какие существуют методы оптимизации для решения задач линейного целочисленного программирования?

Существуют различные методы оптимизации для решения задач линейного целочисленного программирования, включая методы полного перебора, методы ветвей и границ, методы динамического программирования, методы эволюционного поиска и многие другие.

Какой метод оптимизации является наиболее эффективным для решения задач линейного целочисленного программирования?

Наиболее эффективный метод оптимизации для решения задач линейного целочисленного программирования зависит от конкретной задачи и ее особенностей. Некоторые методы, такие как методы полного перебора, гарантированно находят оптимальное решение, но требуют больших вычислительных ресурсов. Другие методы, такие как методы ветвей и границ или методы эволюционного поиска, могут давать приближенные решения, но работать значительно быстрее.

Какие применения имеют методы оптимизации для решения задач линейного целочисленного программирования в реальных задачах?

Методы оптимизации для решения задач линейного целочисленного программирования находят широкое применение в различных областях, таких как логистика, производственное планирование, распределение ресурсов, маршрутизация, планирование сетей и другие. Они позволяют оптимизировать процессы, улучшить использование ресурсов, сократить затраты и повысить эффективность работы системы.