Как называются методы оптимизации которые используют только значения функции

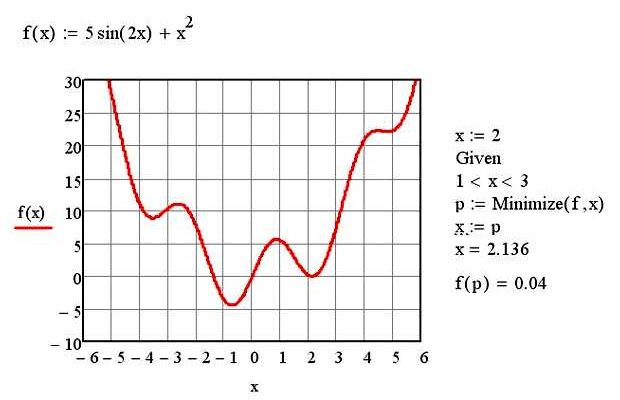
Методы оптимизации на основе значений функции представляют собой класс алгоритмов, используемых для нахождения экстремума (максимума или минимума) функции. Они основаны на вычислении значений функции в различных точках и сравнении их друг с другом.

Один из таких методов оптимизации — метод сканирования (grid search). Он представляет собой перебор значений функции на заданной сетке точек. Суть метода заключается в последовательном вычислении значения функции в каждой точке сетки и сравнении полученных результатов для определения экстремальных точек. Однако этот метод может быть неэффективным при больших размерностях задачи.

Другим методом является метод случайного поиска (random search). Он предполагает случайный выбор точек в пространстве поиска и вычисление значений функции в данных точках. Затем происходит выбор наиболее оптимального значения функции среди полученных.

Методы оптимизации на основе значений функции широко применяются в различных областях, включая машинное обучение, финансовую математику, инженерные задачи и другие. Также существуют разнообразные вариации и комбинации этих методов, позволяющих учесть особенности конкретной задачи и повысить эффективность поиска экстремума.

Методы оптимизации на основе значений функции: как их называют?

Одним из наиболее популярных методов является метод градиентного спуска. Он основан на вычислении градиента функции цели и последовательном движении в направлении, противоположном градиенту. Такой подход позволяет итерационно приближаться к минимуму функции.

Методы на основе обратных квадратичных градиентов

Другим вариантом оптимизации на основе значений функции является метод обратных квадратичных градиентов (OQGM). В этом методе используется комбинация градиента и обновления параметров с использованием квадратичного приближения.

ОQGM широко применяется в задачах оптимизации, требующих квадратичного приближения и обновления шага. Этот метод позволяет достичь схожего результата с методом градиентного спуска, но с меньшим количеством вычислений градиента.

Метод Ньютона-Рафсона

Еще одним методом оптимизации на основе значений функции является метод Ньютона-Рафсона. Он также использует градиент и гессиан функции цели для определения шага обновления параметров.

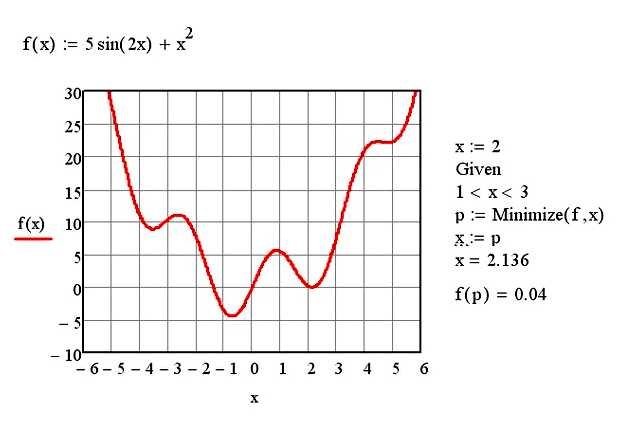
Метод Ньютона-Рафсона является более точным и быстрым по сравнению с методами градиентного спуска и OQGM. Однако он требует более сложных вычислений и может быть менее устойчивым в ситуациях с большим количеством данных.

Бинарный поиск

Принцип работы бинарного поиска основан на том, что список, в котором выполняется поиск, должен быть отсортирован по возрастанию или убыванию. В начале работы алгоритма мы устанавливаем границы индексов, в которых может находиться искомый элемент. Затем мы находим средний индекс между этими границами и сравниваем значение элемента в этой позиции с искомым значением. Если они совпадают, то поиск завершается успешно. Если значение элемента больше искомого, то мы сужаем границы поиска до левой половины списка. Если значение элемента меньше искомого, то сужаем границы до правой половины списка. После сужения границ мы повторяем процесс поиска в новом диапазоне. Поиск завершится, когда границы сомкнутся и индекс вернется к одной точке. Если в этой точке не находится искомый элемент, то его нет в списке.

Бинарный поиск является очень эффективным алгоритмом и позволяет находить элементы в отсортированном списке за время O(log n), где n – количество элементов в списке. Вместо последовательного поиска, который выполняется за время O(n), бинарный поиск позволяет значительно сократить количество операций и повысить эффективность поиска.

Метод Ньютона

Основная идея метода Ньютона заключается в следующем:

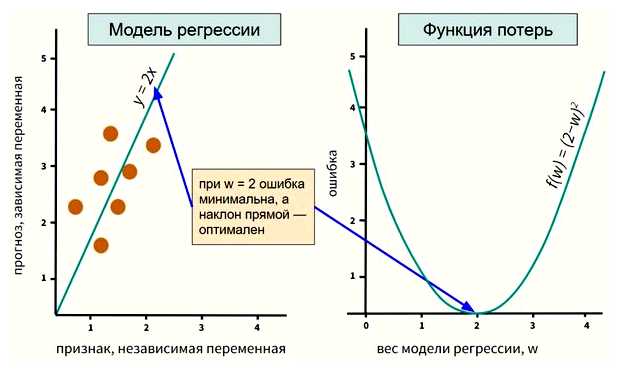
1. Выбирается начальное приближение x0.
2. Проводится локальная аппроксимация функции f(x) в окрестности текущего приближения при помощи квадратичной формы.
3. Находится точка минимума (или максимума) квадратичной формы, что позволяет получить новое приближение x1.
4. Процесс повторяется с новым приближением x1 до достижения необходимой точности.

Метод Ньютона обладает быстрой сходимостью, но имеет несколько ограничений. Одним из них является необходимость вычисления второй производной функции, что может быть затратно и сложно для некоторых функций. Кроме того, метод Ньютона может сходиться к локальному минимуму или максимуму, а не к глобальному.

Тем не менее, метод Ньютона широко применяется в различных областях, таких как оптимизация функций, решение систем нелинейных уравнений и т. д.

Алгоритм Брент

Алгоритм Брент является итеративным методом, который на каждой итерации выбирает новое приближение оптимальной точки. Он использует три значения функции в текущей и предыдущих точках, чтобы определить следующую точку для проверки.

Ключевой идеей алгоритма Брента является интерполяция полиномом второй степени через три точки и использование этого полинома для нахождения следующей точки. Это позволяет алгоритму быстро сходиться к оптимальной точке функции.

Алгоритм Брента является эффективным и надежным методом оптимизации на основе значений функции. Он может использоваться для решения различных задач, таких как минимизация ошибки, поиск экстремума или поиск глобального минимума. В сравнении с другими методами оптимизации, алгоритм Брента обладает преимуществами высокой точности и скорости сходимости.

Вопрос-ответ:

Какие методы оптимизации на основе значений функции существуют?

Существует большое количество методов оптимизации на основе значений функции. Некоторые из них: метод случайного поиска, метод Нелдера-Мида, метод Дэвиса-Свенна-Беккера, методы оптимизации с использованием генетических алгоритмов и многие другие.

Что представляет собой метод случайного поиска?

Метод случайного поиска — это алгоритм оптимизации, в котором решение ищется путем случайной генерации точек в пространстве параметров. После генерации точек вычисляется значение функции в каждой точке, и выбирается точка с наименьшим значением функции. Этот процесс повторяется множество раз, в результате чего найденная точка становится приближенным оптимальным решением.

Как работает метод Нелдера-Мида?

Метод Нелдера-Мида — это итерационный алгоритм оптимизации, который использует комбинацию симплексных операций для приближения к оптимальному решению. На каждой итерации алгоритм использует набор точек, называемых симплексом, и вычисляет значения функции в каждой точке. Затем алгоритм производит симплексные операции, такие как отражение, сжатие и расширение, чтобы улучшить приближение к оптимальному решению.

Какие преимущества и недостатки методов оптимизации с использованием генетических алгоритмов?

Преимущества генетических алгоритмов включают их способность работать с многомерными пространствами параметров и находить глобальные оптимумы, а также их способность обрабатывать нелинейные, недифференцируемые функции. Однако, недостатками методов оптимизации с использованием генетических алгоритмов являются их временные затраты, необходимость подбора параметров и потенциальная сложность сходимости к оптимальному решению.

Можно ли совмещать разные методы оптимизации на основе значений функции?

Да, возможно совмещать разные методы оптимизации на основе значений функции. Некоторые алгоритмы оптимизации, такие как гибридные методы, комбинируют несколько методов для повышения эффективности поиска оптимального решения. Например, можно применить метод случайного поиска для быстрого приближения к оптимальному решению, а затем использовать метод Нелдера-Мида для его уточнения.