Оптимизация первого порядка — это широко распространенный подход к решению задач оптимизации, который основывается на производной функции цели. В этой статье мы рассмотрим несколько методов оптимизации первого порядка, их названия и особенности.
Один из самых популярных методов оптимизации первого порядка — градиентный спуск. Этот метод основан на итерационном генерировании последовательности точек, которые приближенно оптимизируют функцию цели. Основная идея градиентного спуска состоит в том, чтобы двигаться в направлении, противоположном градиенту функции. Ключевое преимущество этого метода — его простота реализации и эффективность в случае выпуклых функций.
Еще одним интересным методом оптимизации первого порядка является метод наискорейшего спуска. В отличие от градиентного спуска, этот метод выбирает шаг так, чтобы достичь минимума функции цели за наименьшее количество итераций. Основная идея метода наискорейшего спуска состоит в том, чтобы на каждой итерации выбирать оптимальный шаг для движения по направлению, противоположному градиенту функции. Это позволяет достичь более быстрой сходимости и улучшить скорость сходимости в случае нелинейных функций.
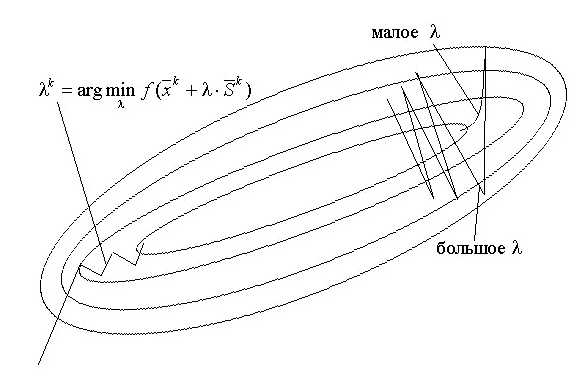
Также стоит упомянуть метод сопряженных градиентов, который широко применяется в задачах оптимизации с квадратичной функцией цели. Этот метод основан на поиске последовательности точек, которые приближенно оптимизируют функцию цели. Чтобы достичь минимума, метод сопряженных градиентов комбинирует информацию о градиентах функции и о предыдущих шагах оптимизации. Это позволяет сократить количество итераций для достижения оптимального решения и повысить эффективность метода.
- Методы оптимизации первого порядка: обзор
- Названия методов оптимизации первого порядка
- Вопрос-ответ:
- Какие методы оптимизации первого порядка существуют?
- В чем особенности градиентного спуска?
- Чем отличается стохастический градиентный спуск от обычного градиентного спуска?
- Как работает метод Ньютона?
- Какие есть вариации метода Ньютона?
- Какие существуют методы оптимизации первого порядка?
Методы оптимизации первого порядка: обзор
Основная идея методов оптимизации первого порядка заключается в поиске локального экстремума функции путём последовательных приближений. В этих методах используется только информация о первых производных функции, что делает их отличительной особенностью от методов более высоких порядков.
Среди наиболее распространенных методов оптимизации первого порядка можно выделить следующие:
- Метод градиентного спуска: широко применяется для минимизации функций. Основная идея заключается в продвижении в направлении антиградиента функции для поиска минимума.
- Метод сопряженных градиентов: оптимизирует квадратичные функции и предоставляет решение в точности после m итераций для функций m переменных.
- Метод Ньютона: используется для минимизации функций с гладкими гессианами. За счет использования гессиана функции, метод Ньютона способен находить аппроксимацию к минимуму с более высокой скоростью сходимости, чем метод градиентного спуска.
- Метод Бройдена-Флетчера-Гольдфарба-Шанно (BFGS): является одним из наиболее популярных методов квазиньютоновского типа. Используется для минимизации негладких функций и показывает высокую скорость сходимости.
- Метод субградиентного спуска: применяется для оптимизации функций субдифференциалы которых определены).

Выбор конкретного метода оптимизации первого порядка зависит от множества факторов, таких как свойства оптимизируемой функции, желаемая точность решения, вычислительные ресурсы и т.д. Каждый из этих методов имеет свои особенности и области применения.

В итоге, методы оптимизации первого порядка играют важную роль в решении различных задач оптимизации, будь то поиск минимума или максимума функции. Знание и понимание особенностей этих методов позволяет эффективно решать задачи оптимизации в различных областях науки и промышленности.

Названия методов оптимизации первого порядка
Ниже приведены некоторые из наиболее известных методов оптимизации первого порядка:
| Градиентный спуск | Использует градиент функции для определения направления наискорейшего убывания итерационного процесса |
| Метод наискорейшего спуска | В качестве направления оптимизации выбирается противоположный градиенту функции в текущей точке |
| Метод сопряженных градиентов | Работает с квадратичными функциями и обеспечивает оптимальность на каждой итерации |
| Метод Ньютона | Использует информацию о градиенте и гессиане функции для быстрой сходимости |
| Метод Левенберга-Марквардта | Хорошо подходит для решения задач нелинейной оптимизации и нахождения решений нелинейных систем уравнений |
Вопрос-ответ:
Какие методы оптимизации первого порядка существуют?
Существует несколько методов оптимизации первого порядка, таких как градиентный спуск, стохастический градиентный спуск, метод Ньютона и его вариации.

В чем особенности градиентного спуска?
Градиентный спуск является итерационным методом оптимизации, основанным на вычислении градиента функции и изменении значения переменных в направлении антиградиента. Он широко применяется в машинном обучении и глубоком обучении.
Чем отличается стохастический градиентный спуск от обычного градиентного спуска?
Стохастический градиентный спуск является вариацией обычного градиентного спуска, в которой градиенты вычисляются не на всем наборе данных, а только на небольших случайно выбранных подмножествах. Это позволяет ускорить вычисления и снизить требования к памяти.
Как работает метод Ньютона?
Метод Ньютона является итерационным методом оптимизации, основанным на использовании второй производной функции (гессиана) для нахождения оптимального значения. Он может сходиться быстрее, чем градиентный спуск, но требует вычисления и обращения гессиана, что может быть вычислительно затратно.
Какие есть вариации метода Ньютона?
Существует несколько вариаций метода Ньютона, таких как метод сопряженных градиентов, квазиньютоновские методы и метод Бройдена-Флетчера-Гольдфарба-Шанно (BFGS). Эти вариации основываются на аппроксимации гессиана или его обратного.
Какие существуют методы оптимизации первого порядка?
Существует несколько методов оптимизации первого порядка, включая метод градиентного спуска, метод наискорейшего спуска, метод сопряженных градиентов.